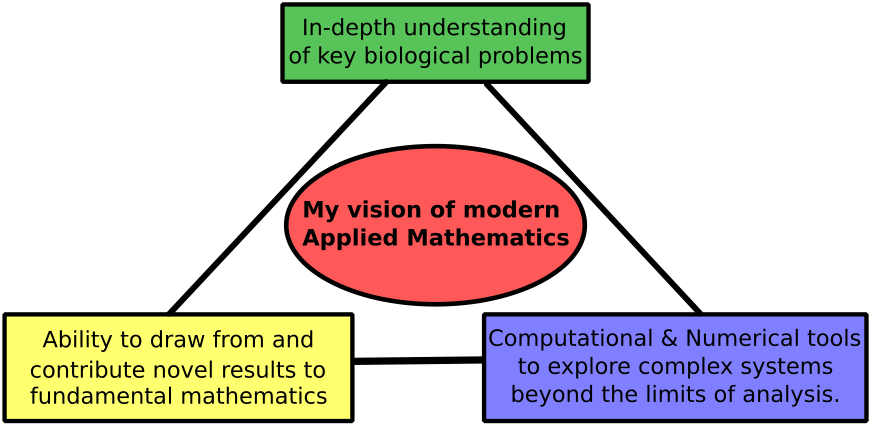
I am an applied mathematician, building bridges between the mathematical, computational, and biological sciences. My strong foundations in each, allow me to identify key biological problems, draw on and contribute to theoretical mathematical foundations, and develop advanced computational tools.
Swarms, flocks, and human societies all exhibit complex collective behaviours. I am interested in collective cell behaviours, which I view as swarms with a twist:
- Cells are not simply point-like particles but have spatial extent;
- Interactions between cells go beyond simple attraction-repulsion; and
- Cells “live” in a regime where friction dominates over inertia.
Examples include: wound healing, embryogenesis (normal development), the immune response, and cancer metastasis. I use mathematical modelling and computational biology to uncover the universal principles how biological, physical, and chemical factors shape biological tissues.
Interactions in tissues range over several orders of magnitude in time and spatial scales. Distinct mathematical frameworks are appropriate for specific levels of detail. For instance, differential equations (DEs), tracking changes in cell (or protein) densities, are suitable for describing large populations. I use dynamical systems, bifurcation theory, and group theory to analyse nonlocal DEs. On the other hand, to track the motion, behaviour, or forces produced by individual cells, a more detailed cell-based computational framework is needed. I refer to such models as cell-based models (CBMs).
Updates
- Our book on bifurcations and symmetries in non-local cell adhesion models is out!
- Our review on computational and mathematical models of cell migration is published.