Non-local models of cell-cell adhesion
Published:
When cells in a tissue exert traction forces, they pull on one another and on the underlying matrix, much like a tug of war. Since cells can extend long protrusions (over several cell diameters), such effects act over long distances (nonlocal), and not simply by neighbour-to-neighbour (local) contact. But most traditional continuum models (PDEs) can only describe local interactions. I use integro-PDEs to capture these nonlocal mechanical tissue stresses. The prototypical cell adhesion model is:
\[\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2} - \alpha \frac{\partial}{\partial x} \left( u(x,t) \int_{-R}^{R} h(u(x+r,t))\Omega(r)\, \mathrm{d} r \right),\]where $u(x,t)$ is the cell density at location $x$ and time $t$, $R$ the cell sensing radius, $\alpha$ the homotypic adhesion strength, $\omega(r)$ an even function, and $h(u)$ a function describing adhesion bond kinetics.
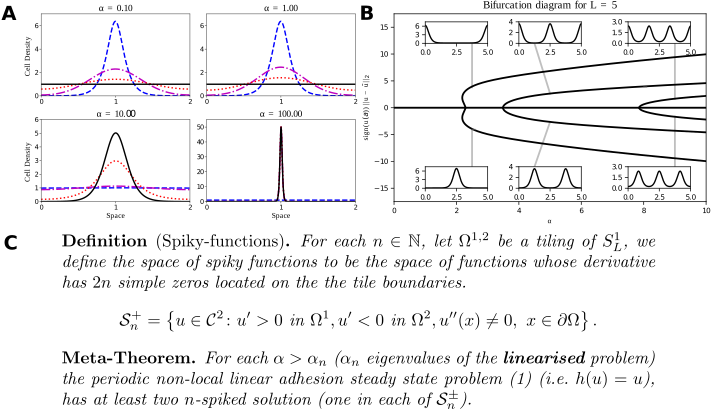
A: Typical solutions of the Armstrong adhesion model for varying $\alpha$. The initial condition is in blue (dashed), the steady state solution is in black (solid). The remaining curves are intermediate times. A bifurcation occurs between $\alpha = 1$ and $\alpha=10$. Numerical solution via a finite volume scheme. (w. ROWMAP integrator). B: Bifurcation diagram of the linear Armstrong model via continuation and spectral collocation using my toolbox. The insets show typical solutions. C: My global bifurcation result, classifying solutions along branches, written as a “meta-theorem”. For details click here.
Publications
- Non-local cell adhesion models: Symmetries and bifurcations in 1-D
- Derivation of non-local population models from a stochastic space-jump process.
- Construction and existence of solution with no-flux boundary conditions.
- My doctoral dissertation on integro-partial differential equation models for cell-cell adhesion and their applications.
- Adhesion-driven patterns in a calcium-dependent model of cancer cell movement
