Non-Local Cell Adhesion Models: Steady States and Bifurcations
Published in arXiv, 2020
Recommended citation: Buttenschön, A., and Hillen, T. arXiv preprint arXiv:2001.00286. (2020) https://arxiv.org/abs/2001.00286
</br>
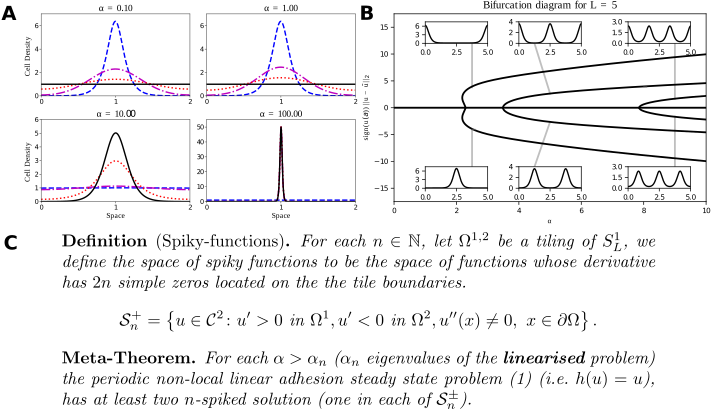
Abstract: In this manuscript, we consider the modelling of cellular adhesions, which is a key interaction between biological cells. Continuum models of the diffusion-advection-reaction type have long been used in tissue modelling. In 2006, Armstrong, Painter, and Sherratt proposed an extension to take adhesion effects into account. The resulting equation is a non-local advection-diffusion equation. While immensely successful in applications, the development of mathematical theory pertaining to steady states and pattern formation is lacking. The mathematical analysis of the non-local adhesion model is challenging. In this monograph, we contribute to the analysis of steady states and their bifurcation structure. The importance of steady-states is that these are the patterns observed in nature and tissues (e.g. cell-sorting experiments). In the case of periodic boundary conditions, we combine global bifurcation results pioneered by Rabinowitz, equivariant bifurcation theory, and the mathematical properties (maximum principle) of the non-local term to obtain a global bifurcation result for the branches of non-trivial solutions.
This publication is part of the Non-local models of cell-cell adhesion project.