Development of mathematical tools for (non-local) reaction-advection-diffusion equations
Published:
Under construction.
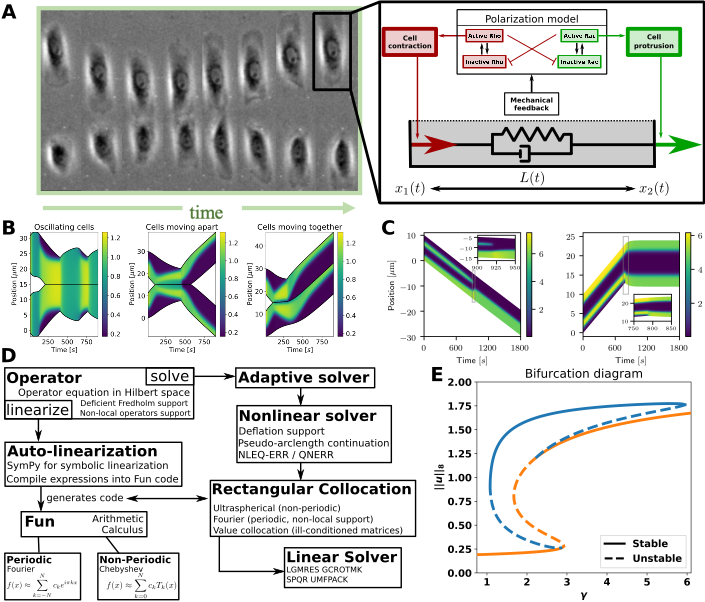
My cell repolarization / signalling model. A: Left: Cell collision experiment (Desai et al. 2013). Right: My mechanochemical model of a 1D cell has two modules: a polarization model, and visco-elastic “spring” connecting the cell’s edges. The polarization model describes intra-cellular proteins resulting in forces on the cell’s edges. B: Cell collisions in my model. C: Intra-cellular pattern formation determines cell behaviour. D: My modular ODE-iPDE analysis toolbox (based on NumPy). Symbolic linearization allows adoption to other spatial systems. E: Bifurcation diagram of a polarization model created by my toolbox. The “S-branch” consists of constant solutions, while the others are polarized states (see C).
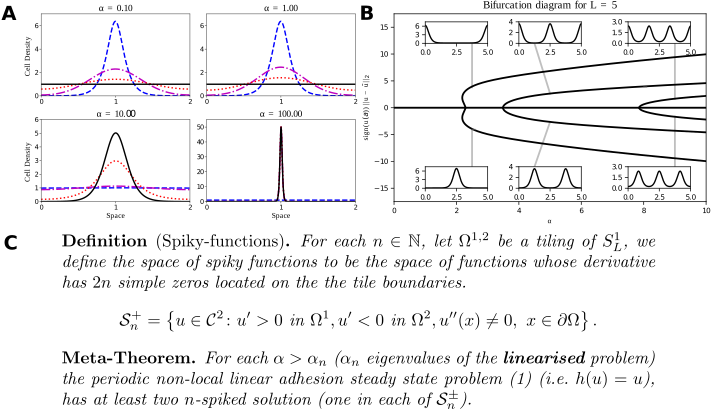
A: Typical solutions of the Armstrong adhesion model for varying $\alpha$. The initial condition is in blue (dashed), the steady state solution is in black (solid). The remaining curves are intermediate times. A bifurcation occurs between $\alpha = 1$ and $\alpha=10$. Numerical solution via a finite volume scheme. (w. ROWMAP integrator). B: Bifurcation diagram of the linear Armstrong model via continuation and spectral collocation using my toolbox. The insets show typical solutions. C: My global bifurcation result, classifying solutions along branches, written as a “meta-theorem”.
