The Interpolation Problem¶
Problem: Given distinct points , find a polynomial such that:
Proof 1
Existence: The Lagrange form (below) explicitly constructs such a polynomial.
Uniqueness: Suppose and are both polynomials of degree at most interpolating the same data. Consider the difference .
is a polynomial of degree at most
for all
So has roots. But a nonzero polynomial of degree can have at most roots. Therefore , which means .
Lagrange Basis Polynomials¶
For nodes , define the Lagrange basis polynomial:
Key property:
The interpolating polynomial is then:
Barycentric Interpolation¶
Can we do better? Yes—by algebraically reorganizing the Lagrange formula, we obtain the barycentric form, which resolves all three issues while computing the same polynomial.
The Node Polynomial¶
Define the node polynomial:
Its derivative at a node is:
This lets us rewrite the Lagrange basis as:
Barycentric Weights¶
Define the barycentric weights:
Then the Lagrange basis becomes:
First Barycentric Formula¶
Substituting into the interpolant gives the first barycentric formula:
Once the weights are known (computed once in time), evaluating costs only .
Second Barycentric Formula¶
An even more elegant formula comes from the identity (the Lagrange polynomials form a partition of unity—they interpolate the constant function 1).
Dividing the interpolant by this identity:
Why ?
The function (constant) is interpolated by itself. Since for all :
This follows from the uniqueness of polynomial interpolation.
Advantages¶
per evaluation after preprocessing for weights
Numerically stable even for large
Adding a point only requires updating weights
Implementation¶
def bary_weights(x):
"""Compute barycentric weights for nodes x."""
n = len(x)
w = np.ones(n)
for j in range(n):
for i in range(n):
if i != j:
w[j] /= (x[j] - x[i])
return w
def bary_interp(xeval, x, y, w):
"""Evaluate interpolant at xeval using barycentric formula."""
# Handle evaluation at nodes
for j, xj in enumerate(x):
if np.isclose(xeval, xj):
return y[j]
terms = w / (xeval - x)
return np.dot(terms, y) / np.sum(terms)Chebyshev Points and Barycentric Weights¶
For Chebyshev points, the barycentric weights have a remarkably simple closed form:
This makes Chebyshev interpolation especially efficient—no weight computation needed!
def cheb_bary_weights(n):
"""Barycentric weights for Chebyshev points."""
w = np.ones(n+1)
w[0] = 0.5
w[-1] = 0.5
w[1::2] *= -1
return wNumerical Stability¶
The two barycentric formulas have different stability properties. The following results are due to Higham (2004).
Backward Stability of the First Formula¶
Forward Stability of the Second Formula¶
Comparison¶
| Formula | Stability Type | Best For |
|---|---|---|
| First (modified Lagrange) | Backward stable | Extrapolation, any nodes |
| Second (barycentric) | Forward stable | Interpolation with good nodes |
Why Scale Invariance Matters¶
The second barycentric formula is scale invariant: we can multiply all weights by any nonzero constant without changing the result:
This means we can rescale weights to avoid overflow, which is critical for large .
Warning: Equispaced Points¶
For equispaced points, the weights grow like:
This grows exponentially, making polynomial interpolation through equispaced points numerically unstable—even with the barycentric formula. This is separate from (but compounds) Runge’s phenomenon.
Runge’s Phenomenon: A Warning¶
Consider on .
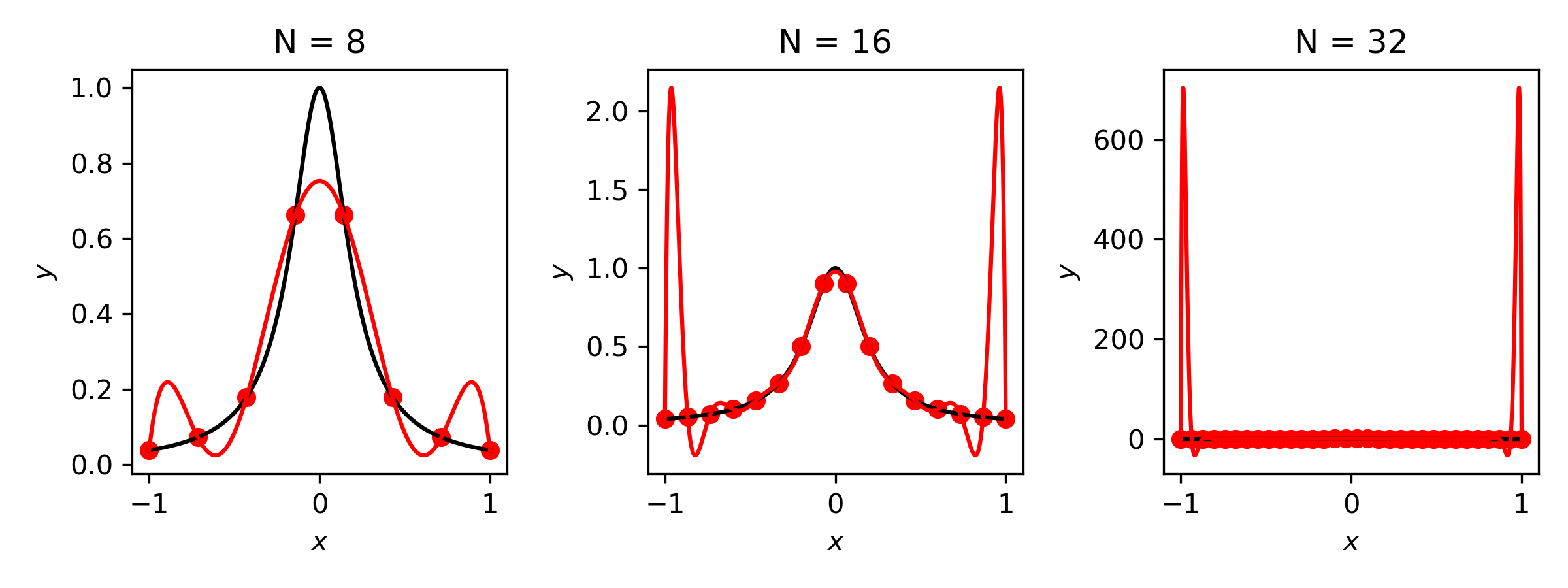
Runge’s phenomenon: Polynomial interpolation of through equally spaced nodes. As the degree increases, the interpolant develops large oscillations near the boundaries, despite the function being smooth.
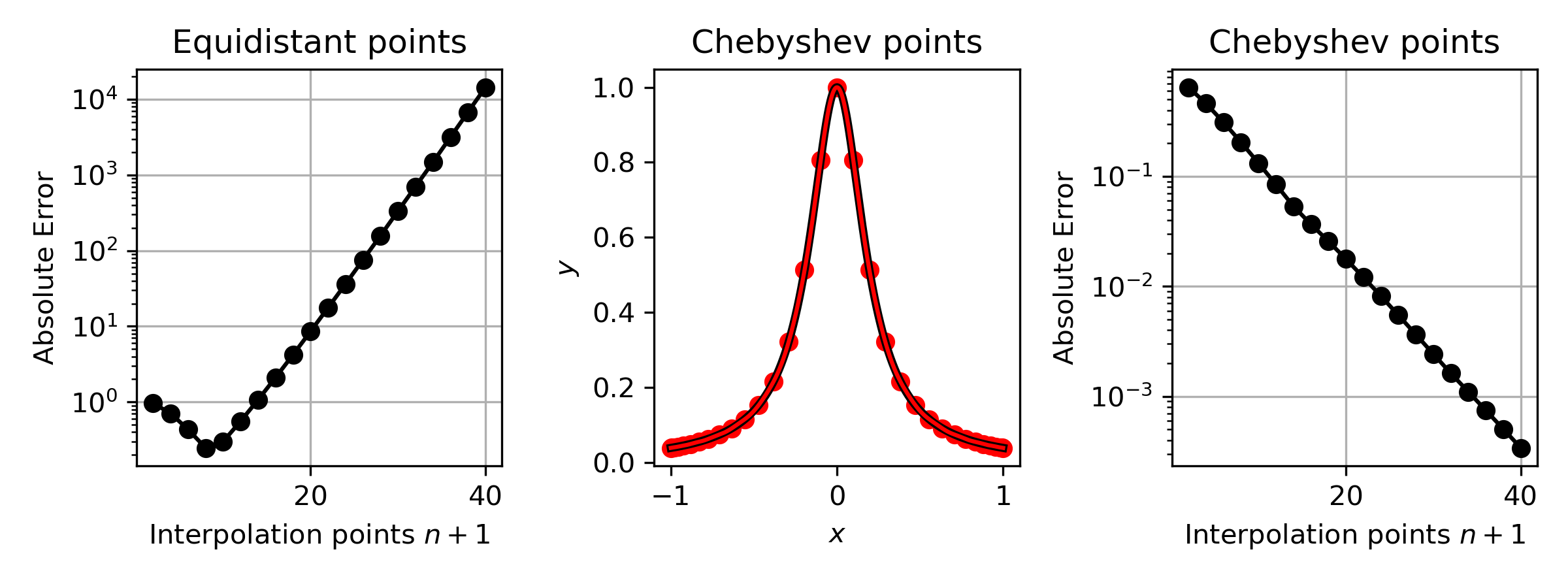
Interpolation error comparison: (Left) Equidistant points cause error to grow exponentially with . (Center) Chebyshev points cluster near endpoints. (Right) Chebyshev interpolation error decreases exponentially—the hallmark of spectral accuracy.
| Nodes | Error as |
|---|---|
| Equally spaced | Grows without bound |
| Chebyshev | Decreases exponentially |
# Equally spaced: error GROWS
x_eq = np.linspace(-1, 1, n)
f_eq = 1/(1 + 25*x_eq**2)
# Interpolant oscillates wildly near boundaries!
# Chebyshev: error DECREASES
x_cheb = np.cos(np.pi * np.arange(n) / (n-1))
f_cheb = 1/(1 + 25*x_cheb**2)
# Smooth, accurate approximationThe lesson: node placement matters. Chebyshev nodes cluster near the endpoints, exactly where equally spaced nodes cause trouble.
Use barycentric interpolation. It’s the standard in modern software (Chebfun, etc.).
References¶
- Higham, N. J. (2004). The numerical stability of barycentric Lagrange interpolation. IMA Journal of Numerical Analysis, 24(4), 547–556. 10.1093/imanum/24.4.547
- Berrut, J.-P., & Trefethen, L. N. (2004). Barycentric Lagrange interpolation. SIAM Review, 46(3), 501–517. 10.1137/S0036144502417715
- Webb, M., Trefethen, L. N., & Gonnet, P. (2012). Stability of barycentric interpolation formulas for extrapolation. SIAM Journal on Scientific Computing, 34(6), A3009–A3015. 10.1137/110848797