Numerical Differentiation University of Massachusetts Amherst
Suppose we have a function f ( x ) f(x) f ( x ) x 0 x_0 x 0 y = f ( x ) y = f(x) y = f ( x ) x 0 x_0 x 0
Recall the limit definition of the derivative:
f ′ ( x 0 ) = lim h → 0 f ( x 0 + h ) − f ( x 0 ) h f'(x_0) = \lim_{h\to 0} \frac{f(x_0 + h) - f(x_0)}{h} f ′ ( x 0 ) = h → 0 lim h f ( x 0 + h ) − f ( x 0 ) The left-hand side is the slope of the tangent line, while the right-hand side is the limit of the slope of the secant line connecting the points ( x 0 , f ( x 0 ) ) (x_0, f(x_0)) ( x 0 , f ( x 0 )) ( x 0 + h , f ( x 0 + h ) ) (x_0 + h, f(x_0 + h)) ( x 0 + h , f ( x 0 + h ))
This suggests we can approximate the derivative using:
f ′ ( x 0 ) ≈ f ( x 0 + h ) − f ( x 0 ) h f'(x_0) \approx \frac{f(x_0 + h) - f(x_0)}{h} f ′ ( x 0 ) ≈ h f ( x 0 + h ) − f ( x 0 ) for h h h how accurate is this approximation?
Error Analysis ¶ The forward difference approximation satisfies:
f ( x 0 + h ) − f ( x 0 ) h = f ′ ( x 0 ) + E ( h ) \frac{f(x_0 + h) - f(x_0)}{h} = f'(x_0) + E(h) h f ( x 0 + h ) − f ( x 0 ) = f ′ ( x 0 ) + E ( h ) where the error is:
E ( h ) = − h 2 f ′ ′ ( ξ ) = O ( h ) E(h) = -\frac{h}{2} f''(\xi) = \mathcal{O}(h) E ( h ) = − 2 h f ′′ ( ξ ) = O ( h ) for some ξ ∈ ( x 0 , x 0 + h ) \xi \in (x_0, x_0 + h) ξ ∈ ( x 0 , x 0 + h ) first-order in h h h
Proof 1
Using Taylor’s theorem with k = 1 k = 1 k = 1
f ( x 0 + h ) = f ( x 0 ) + f ′ ( x 0 ) h + f ′ ′ ( ξ ) 2 h 2 f(x_0 + h) = f(x_0) + f'(x_0) h + \frac{f''(\xi)}{2} h^2 f ( x 0 + h ) = f ( x 0 ) + f ′ ( x 0 ) h + 2 f ′′ ( ξ ) h 2 where ξ ∈ ( x 0 , x 0 + h ) \xi \in (x_0, x_0 + h) ξ ∈ ( x 0 , x 0 + h )
Substituting into our secant line approximation:
f ( x 0 + h ) − f ( x 0 ) h = 1 h ( f ( x 0 ) + h f ′ ( x 0 ) + 1 2 h 2 f ′ ′ ( ξ ) − f ( x 0 ) ) = f ′ ( x 0 ) + 1 2 h f ′ ′ ( ξ ) \begin{split}
\frac{f(x_0 + h) - f(x_0)}{h} &= \frac{1}{h}\left( f(x_0) + h f'(x_0) + \frac{1}{2} h^2 f''(\xi) - f(x_0) \right) \\
&= f'(x_0) + \frac{1}{2} h f''(\xi)
\end{split} h f ( x 0 + h ) − f ( x 0 ) = h 1 ( f ( x 0 ) + h f ′ ( x 0 ) + 2 1 h 2 f ′′ ( ξ ) − f ( x 0 ) ) = f ′ ( x 0 ) + 2 1 h f ′′ ( ξ ) Remark 1 (Computational Verification)
To verify the error theory: if E ( h ) = C h E(h) = Ch E ( h ) = C h log E = log C + log h \log E = \log C + \log h log E = log C + log h
Plot log E \log E log E log h \log h log h straight line with slope 1 .
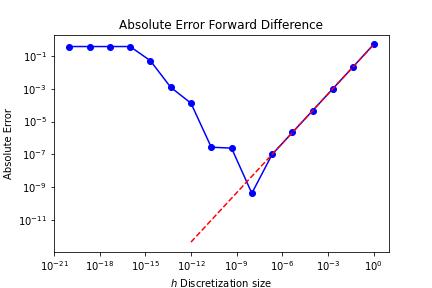
The absolute error of the forward difference approximation of the derivative for sin ( x 0 ) \sin(x_0) sin ( x 0 ) x 0 = 1.2 x_0 = 1.2 x 0 = 1.2
The Round-off Error Trade-off ¶ The plot above shows something surprising: the error increases for very small h h h
This is our first encounter with a fundamental phenomenon in scientific computing: round-off error . When h h h f ( x 0 + h ) ≈ f ( x 0 ) f(x_0 + h) \approx f(x_0) f ( x 0 + h ) ≈ f ( x 0 ) h h h
In the next chapter on floating-point arithmetic , we’ll learn:
Why computers can’t represent most real numbers exactly
What machine epsilon is and why it’s approximately 10-16 for double precision
How to find the optimal step size that balances truncation and round-off error
For now, the practical takeaway is: smaller h h h . For first-order finite differences, h ≈ 1 0 − 8 h \approx 10^{-8} h ≈ 1 0 − 8
The forward difference only uses information to the right of x 0 x_0 x 0 both sides should give a better approximation to the tangent line—the secant line through ( x 0 − h , f ( x 0 − h ) ) (x_0 - h, f(x_0 - h)) ( x 0 − h , f ( x 0 − h )) ( x 0 + h , f ( x 0 + h ) ) (x_0 + h, f(x_0 + h)) ( x 0 + h , f ( x 0 + h ))
Proof 2
We expand both f ( x 0 + h ) f(x_0 + h) f ( x 0 + h ) f ( x 0 − h ) f(x_0 - h) f ( x 0 − h )
f ( x 0 ± h ) = f ( x 0 ) ± h f ′ ( x 0 ) + h 2 2 f ′ ′ ( x 0 ) ± h 3 6 f ′ ′ ′ ( ξ ± ) + O ( h 4 ) f(x_0 \pm h) = f(x_0) \pm h f'(x_0) + \frac{h^2}{2}f''(x_0) \pm \frac{h^3}{6} f'''(\xi^{\pm}) + O(h^4) f ( x 0 ± h ) = f ( x 0 ) ± h f ′ ( x 0 ) + 2 h 2 f ′′ ( x 0 ) ± 6 h 3 f ′′′ ( ξ ± ) + O ( h 4 ) Substituting into the central difference formula:
f ( x 0 + h ) − f ( x 0 − h ) 2 h = 1 2 h ( 2 h f ′ ( x 0 ) + h 3 6 ( f ′ ′ ′ ( ξ + ) + f ′ ′ ′ ( ξ − ) ) + O ( h 5 ) ) = f ′ ( x 0 ) + h 2 12 ( f ′ ′ ′ ( ξ − ) + f ′ ′ ′ ( ξ + ) ) + O ( h 4 ) \begin{split}
\frac{f(x_0 + h) - f(x_0 - h)}{2h}
&= \frac{1}{2h}\left( 2hf'(x_0) + \frac{h^3}{6}\left( f'''(\xi^+) + f'''(\xi^-) \right) + O(h^5)\right) \\
&= f'(x_0) + \frac{h^2}{12} \left( f'''(\xi^-) + f'''(\xi^+) \right) + O(h^4)
\end{split} 2 h f ( x 0 + h ) − f ( x 0 − h ) = 2 h 1 ( 2 h f ′ ( x 0 ) + 6 h 3 ( f ′′′ ( ξ + ) + f ′′′ ( ξ − ) ) + O ( h 5 ) ) = f ′ ( x 0 ) + 12 h 2 ( f ′′′ ( ξ − ) + f ′′′ ( ξ + ) ) + O ( h 4 ) Why the improvement? The even-powered terms (h 2 , h 4 , … h^2, h^4, \ldots h 2 , h 4 , … cancel due to symmetry.
Central finite difference error for approximating tan ′ ( 0.2 ) \tan'(0.2) tan ′ ( 0.2 ) O ( h 2 ) O(h^2) O ( h 2 ) h ≈ 1 0 − 6 h \approx 10^{-6} h ≈ 1 0 − 6
Comparison: Forward vs Central ¶ Method Formula Error Order Forward f ( x 0 + h ) − f ( x 0 ) h \frac{f(x_0 + h) - f(x_0)}{h} h f ( x 0 + h ) − f ( x 0 ) O ( h ) O(h) O ( h ) 1st Central f ( x 0 + h ) − f ( x 0 − h ) 2 h \frac{f(x_0 + h) - f(x_0 - h)}{2h} 2 h f ( x 0 + h ) − f ( x 0 − h ) O ( h 2 ) O(h^2) O ( h 2 ) 2nd
Example 1 (Accuracy Comparison)
For h = 0.01 h = 0.01 h = 0.01
The central difference is 100× more accurate for the same step size!
Remark 2 (Optimal Step Size for Central Differences)
The total error (truncation + roundoff) is:
E ( h ) = M 0 μ h + M 1 h 2 E(h) = \frac{M_0 \mu}{h} + M_1 h^2 E ( h ) = h M 0 μ + M 1 h 2 Minimizing gives h opt ≈ μ 1 / 3 ≈ 6 × 1 0 − 6 h_{\text{opt}} \approx \mu^{1/3} \approx 6 \times 10^{-6} h opt ≈ μ 1/3 ≈ 6 × 1 0 − 6
This is larger than for forward differences because truncation error decreases faster (h 2 h^2 h 2 h h h
Second Derivative Approximation ¶ Proof 3
Adding the Taylor expansions (instead of subtracting):
f ( x 0 + h ) + f ( x 0 − h ) = 2 f ( x 0 ) + h 2 f ′ ′ ( x 0 ) + O ( h 4 ) f(x_0 + h) + f(x_0 - h) = 2f(x_0) + h^2 f''(x_0) + O(h^4) f ( x 0 + h ) + f ( x 0 − h ) = 2 f ( x 0 ) + h 2 f ′′ ( x 0 ) + O ( h 4 ) Solving for f ′ ′ ( x 0 ) f''(x_0) f ′′ ( x 0 )
This formula is fundamental in numerical PDE s—it’s the discrete Laplacian in one dimension.
Summary ¶ Method Formula Error Order Forward difference f ( x + h ) − f ( x ) h \frac{f(x+h) - f(x)}{h} h f ( x + h ) − f ( x ) O ( h ) O(h) O ( h ) Central difference f ( x + h ) − f ( x − h ) 2 h \frac{f(x+h) - f(x-h)}{2h} 2 h f ( x + h ) − f ( x − h ) O ( h 2 ) O(h^2) O ( h 2 ) Second derivative f ( x + h ) − 2 f ( x ) + f ( x − h ) h 2 \frac{f(x+h) - 2f(x) + f(x-h)}{h^2} h 2 f ( x + h ) − 2 f ( x ) + f ( x − h ) O ( h 2 ) O(h^2) O ( h 2 )
Key principle: Using symmetric stencils improves accuracy, but there are diminishing returns due to round-off error. The optimal step size balances truncation and round-off errors.