Taylor’s Theorem - Introduction to Scientific Computing

Statement of Taylor’s Theorem¶

Suppose we have a function $f(x)$ with $k + 1$ continuous derivatives, and let $x = x_0 + h$ then we can write:

\begin{split} f(x) &= \underbrace{P_k(x)}_{\text{$k$-th Taylor polynomial}} + \underbrace{R_k(x)}_{\text{Remainder or error term}} \\ f(x) &= \sum_{i=0}^{k} \frac{f^{(i)}(x_0)}{i!} (x - x_0)^i + \frac{f^{(k+1)}(\xi)}{(k+1)!}(x - x_0)^{k+1}, \end{split}

(2)

where $\xi \in (x_0, x_0 + h)$ . This means that the approximation error is:

|f(x) - P_k(x)| = |R_k(x)| \quad\implies\quad \sup_{x \in [a, b]} |f(x) - P_k(x)| = \sup_{x \in [a, b]} |R_k(x)|.

(3)

Example 1 (Computing

e

to a Given Accuracy)

Suppose we want to compute the number $e$ to an accuracy of 10^-3.

We can do this by computing a Taylor series for the function $e^x$ . Since we know the value at $x = 0$ , namely $f(0) = e^0 = 1$ , we use that as the point about which we create the Taylor series.

Since $f^{(n)}(x) = e^x$ , we have $f^{(n)}(0) = 1$ for all $n$ .

The $n$ -degree Taylor polynomial is:

T_n(x) = 1 + x + \frac{x^2}{2} + \cdots + \frac{x^n}{n!}

(5)

To estimate the error, we compute the remainder:

R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}x^{n+1}

(6)

where $\xi \in [0, 1]$ . Since $e^x$ is positive and increasing:

\sup_{x \in [0, 1]}|R_n(x)| \leq \frac{e^x}{(n+1)!} \leq \frac{3}{(n+1)!}.

(7)

To achieve the required accuracy:

\sup_{x \in [0, 1]}|R_n(x)| \leq 10^{-3} \quad\implies\quad \frac{3}{(n+1)!} \leq 10^{-3}.

(8)

With some experimentation, we find that the first $n$ for which this inequality holds is $n = 6$ .

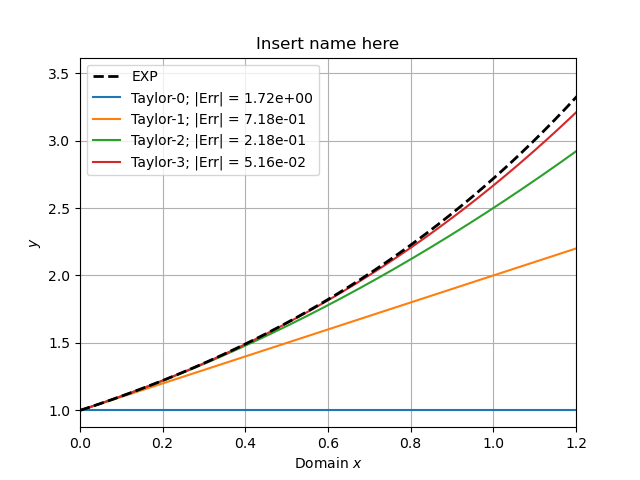
The first four Taylor polynomials P_1, P_2, P_3, P_4 of f(x) = e^x centered at x_0 = 0. The approximations converge to the true function (dashed black) as the degree increases. — The first four Taylor polynomials $P_1, P_2, P_3, P_4$ of $f(x) = e^x$ centered at $x_0 = 0$ . The approximations converge to the true function (dashed black) as the degree increases.

Why Taylor’s Theorem Matters¶

Taylor’s theorem is a workhorse of numerical analysis because:

It allows us to replace complicated functions with polynomials
The remainder term gives us explicit error bounds
It reveals how accuracy depends on the step size $h$

In the next section, we’ll use Taylor’s theorem to derive finite difference approximations for derivatives.