Andreas Buttenschön

Andreas Buttenschön

Assistant Professor in Applied Mathematics at the University of Massachusetts Amherst

Continuum Models Capturing Long-Range Cell Communication

Published:

I develop non-local integro-partial differential equations (iPDEs) where interaction kernels $W(r,p)$ encode both spatial separation and cellular state (such as polarization). This framework provides a rigorous mathematical language for collective cell migration analogous to Green’s functions in classical physics.

When cells in a tissue exert traction forces, they pull on one another and on the underlying matrix, much like a tug of war. Since cells can extend long protrusions (over several cell diameters), such effects act over long distances (nonlocal), and not simply by neighbour-to-neighbour (local) contact. But most traditional continuum models (PDEs) can only describe local interactions. I use integro-PDEs to capture these nonlocal mechanical tissue stresses.

The Mathematical Framework

The prototypical cell adhesion model is:

\[\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2} - \alpha \frac{\partial}{\partial x} \left( u(x,t) \int_{-R}^{R} h(u(x+r,t))\Omega(r)\, \mathrm{d} r \right),\]

where $u(x,t)$ is the cell density at location $x$ and time $t$, $R$ the cell sensing radius, $\alpha$ the homotypic adhesion strength, $\omega(r)$ an even function, and $h(u)$ a function describing adhesion bond kinetics.



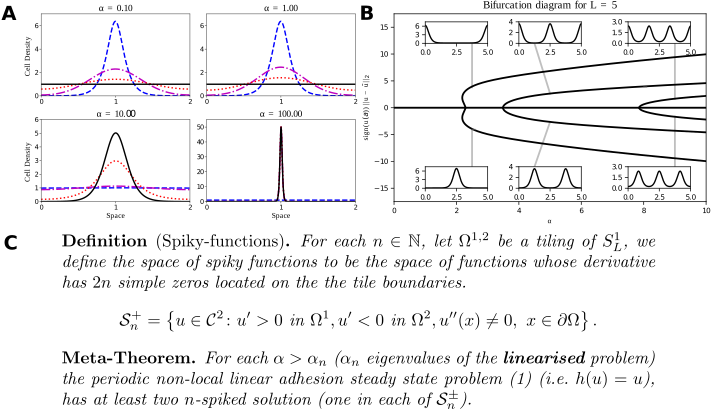
A: Typical solutions of the Armstrong adhesion model for varying $\alpha$. The initial condition is in blue (dashed), the steady state solution is in black (solid). The remaining curves are intermediate times. A bifurcation occurs between $\alpha = 1$ and $\alpha=10$. Numerical solution via a finite volume scheme. B: Bifurcation diagram of the linear Armstrong model via continuation and spectral collocation using my toolbox. The insets show typical solutions. C: My global bifurcation result, classifying solutions along branches, written as a “meta-theorem”.

For details click here.

Key Innovation: State-Dependent Interaction Kernels

By incorporating cellular polarization states into interaction kernels $W(r,p)$, I resolve paradoxes like the “pseudo-inertia” phenomenon where cells in overdamped environments exhibit apparent inertial behavior. This framework enables systematic coarse-graining from cell-based models to continuum descriptions while preserving bifurcation structures and emergent behaviors.

This approach provides a rigorous mathematical language for collective cell migration analogous to Green’s functions in classical physics, enabling cumulative scientific progress where theoretical advances in one biological context immediately benefit all systems sharing the same mathematical structure.

Current Research Directions

From Paradox to Principle

Recent experiments reveal cells exhibit apparent inertial behavior in overdamped environments—a fundamental paradox since Reynolds numbers $\sim 10^{-6}$ make physical inertia negligible. My work demonstrates how polarization-position coupling creates this apparent second-order behavior and identifies symmetry-breaking mechanisms enabling cell entrainment.

Rigorous Coarse-Graining

I develop systematic procedures that preserve bifurcation structure when transitioning from cell-based to continuum models, proving when polarization transport must supplement density evolution to capture collective behaviors.

Publications