Fundamental Subspaces

Every vector in the nullspace is orthogonal to every row of \(A\), in other words the nullspace \(N[A]\) and the row space \(R[A^T]\) are orthogonal complements. Similarly, every vector in the left null space is orthogonal to every column of \(A\), in other words the left nullspace \(N[A^T]\) and the column space \(R[A]\) are orthogonal complements.

Fundamental Subspaces

Let \(A\) be a \(m \times n\) matrix. The fundamental subspaces of \(A\) are \(N[A]\), \(R[A]\), \(N[A^T]\) and \(R[A^T]\).

1. The nullspace of the matrix \(A\) is the space of all vector such that \(Ax = 0\), in other words it contains weights of linear combinations that vanish.

\[ N[A] := \left\{ x \in \mathbb{R}^n : A x = 0 \right\} \subset \mathbb{R}^n. \]

2. The column space or range of the matrix \(A\) is the space of all linear combinations of the columns of \(A\).

\[ R[A] := \left\{ A x : x \in \mathbb{R}^n \right\} \subset \mathbb{R}^m. \]

3. The row space is the space of all linear combinations of the rows of the matrix \(A\), or equivalently it is the space of all the linear combinations of the columns of \(A^T\) (i.e. the column space of \(A^T\)),

\[ R[A^T] := \left\{ A^T x : x \in \mathbb{R}^m \right\} \subset \mathbb{R}^n. \]

4. The left nullspace of \(A\) is the null space of \(A^T\).

\[ N[A^T] := \left\{ y \in \mathbb{R}^m : A^T y = 0 \right\} \subset \mathbb{R}^m. \]

It is called the left nullspace since \((A^T y)^T = 0^T \implies y^T A = 0\), note the multiplication from the left. In other words, it contains the weights so that a linear combination of the rows of \(A\) is zero.

Find the null space, column space, row space, and left null space of a matrix

\[\begin{split} A = \begin{bmatrix} 2 & 4 & 12 \\ 2 & 1 & 3 \end{bmatrix} \end{split}\]

Solution

Nullspace:

\[\begin{split} \begin{bmatrix} 2 & 4 & 12 & 0 \\ 2 & 1 & 3 & 0\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 2 & 6 & 0 \\ 2 & 1 & 3 & 0\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 2 & 6 & 0 \\ 0 & -3 & -9 & 0\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 2 & 6 & 0 \\ 0 & 1 & 3 & 0\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 3 & 0\end{bmatrix} \end{split}\]

This means that

\[\begin{split} N[A] = \text{span}\left\{\begin{bmatrix} 0 \\ -3 \\ 1\end{bmatrix} \right\} \end{split}\]

rowspace:

\[\begin{split} \begin{bmatrix} 2 & 4 & 12 \\ 2 & 1 & 3\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 3\end{bmatrix} \end{split}\]

This means that

\[\begin{split} R[A] = \text{span}\left\{\begin{bmatrix} 2 \\ 2\end{bmatrix}, \begin{bmatrix} 4 \\ 1\end{bmatrix} \right\} \end{split}\]

Columnspace:

\[\begin{split} A^T = \begin{bmatrix} 2 & 2 \\ 1 & 4 \\ 3 & 12\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 1 \\ 1 & 4 \\ 3 & 12\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 1 \\ 0 & 3 \\ 3 & 12\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 1 \\ 0 & 3 \\ 3 & 12\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 1 \\ 0 & 3 \\ 0 & 9\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 1 \\ 0 & 1 \\ 0 & 9\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 0 & 9\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 0 & 0\end{bmatrix} \end{split}\]

This means that

\[\begin{split} R[A^T] = \text{span}\left\{\begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix}, \begin{bmatrix} 2 \\ 4 \\ 12\end{bmatrix}\right\} \end{split}\]

Left Nullspace:

\[\begin{split} A^T = \begin{bmatrix} 2 & 2 \\ 1 & 4 \\ 3 & 12\end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 0 & 0\end{bmatrix} \end{split}\]

This means that

\[\begin{split} N[A^T] = \text{span}\left\{\begin{bmatrix} 0 \\ 0 \end{bmatrix}\right\} \end{split}\]

Orthogonality of the fundamental subspaces

Let \(A\) be a \(m \times n\) matrix. Then \(N(A) = R(A^T)^{\perp}\) and \(R(A) = N(A^T)^{\perp}\).

---

Proof. The second equality follows from the first by replacing \(A\) with \(A^T\) therefore it is sufficient to prove \(N(A) = R(A^T)^{\perp}\). A general strategy to prove equality of sets is to show that each set contains the other therefore let us prove \(N(A) \subseteq R(A^T)^{\perp}\) and then prove the reverse \(R(A^T)^{\perp} \subseteq N(A)\).

Let \(\boldsymbol{x} \in N(A)\). Then \(A \boldsymbol{x} = \boldsymbol{0}\) therefore \(\langle A \boldsymbol{x} , \boldsymbol{y} \rangle = 0\) for all \(\boldsymbol{y} \in \mathbb{R}^m\). Using properties of the inner product we see that \(\langle \boldsymbol{x} , A^T \boldsymbol{y} \rangle = 0\) for all \(\boldsymbol{y} \in \mathbb{R}^m\) therefore \(\boldsymbol{x} \in R(A^T)^{\perp}\).

Now let \(\boldsymbol{x} \in R(A^T)^{\perp}\). Then \(\langle \boldsymbol{x} , A^T \boldsymbol{y} \rangle = 0\) and so \(\langle A \boldsymbol{x} , \boldsymbol{y} \rangle = 0\) for all \(\boldsymbol{y} \in \mathbb{R}^m\). Choose \(\boldsymbol{y} = A\boldsymbol{x} \in \mathbb{R}^m\) and then \(\langle A \boldsymbol{x} , A \boldsymbol{x} \rangle = 0\). Therefore \(\| A \boldsymbol{x} \| = 0\) and so \(A \boldsymbol{x} = \boldsymbol{0}\) and finally \(\boldsymbol{x} \in N(A)\).

Since \(N(A) \subseteq R(A^T)^{\perp}\) and \(R(A^T)^{\perp} \subseteq N(A)\) we have \(N(A) = R(A^T)^{\perp}\).

Let \(U \subseteq \mathbb{R}^n\) be a subspace. Then

\[ \dim(U) + \dim(U^{\perp}) = n \]

---

Proof. Let \(\dim(U) = m\) and let \(\boldsymbol{u}_1 , \dots, \boldsymbol{u}_m\) be a basis of \(U\) and define

\[\begin{split} A = \begin{bmatrix} & \boldsymbol{u}_1^T & \\ & \vdots & \\ & \boldsymbol{u}_m^T & \end{bmatrix} \end{split}\]

Then \(U = R(A^T)\) and \(U^{\perp} = R(A^T)^{\perp} = N(A)\) and we know \(\mathrm{rank}(A) = m = \dim(U)\) therefore

\[ \dim(U) + \dim(U^{\perp}) = \mathrm{rank}(A) + \dim(N(A)) = n \]

by the Rank-Nullity Theorem.

Let \(A\) be a matrix such that its LU decomposition is of the form

\[\begin{split} A = LU = \begin{bmatrix} 1 & 0 & 0 \\ * & 1 & 0 \\ * & * & 1 \end{bmatrix} \begin{bmatrix} * & * & * & * \\ 0 & * & * & * \\ 0 & 0 & * & * \end{bmatrix} \end{split}\]

where \(*\) denotes a nonzero number. Find the dimension of each subspace \(N(A)\), \(R(A)\), \(N(A^T)\) and \(R(A^T)\).

Clearly \(\dim(N(A)) = 1\) and \(\dim(R(A)) = 3\) therefore

\[ \dim(N(A^T)) = \dim(R(A)^{\perp}) = 3 - 3 = 0 \]

and

\[ \dim(R(A^T)) = \dim(N(A)^{\perp}) = 4 - 1 = 3 \]

Fundamental Subspaces Big Picture

Figure 1: Dimensions and orthogonality for any m by n matrix A of rank r

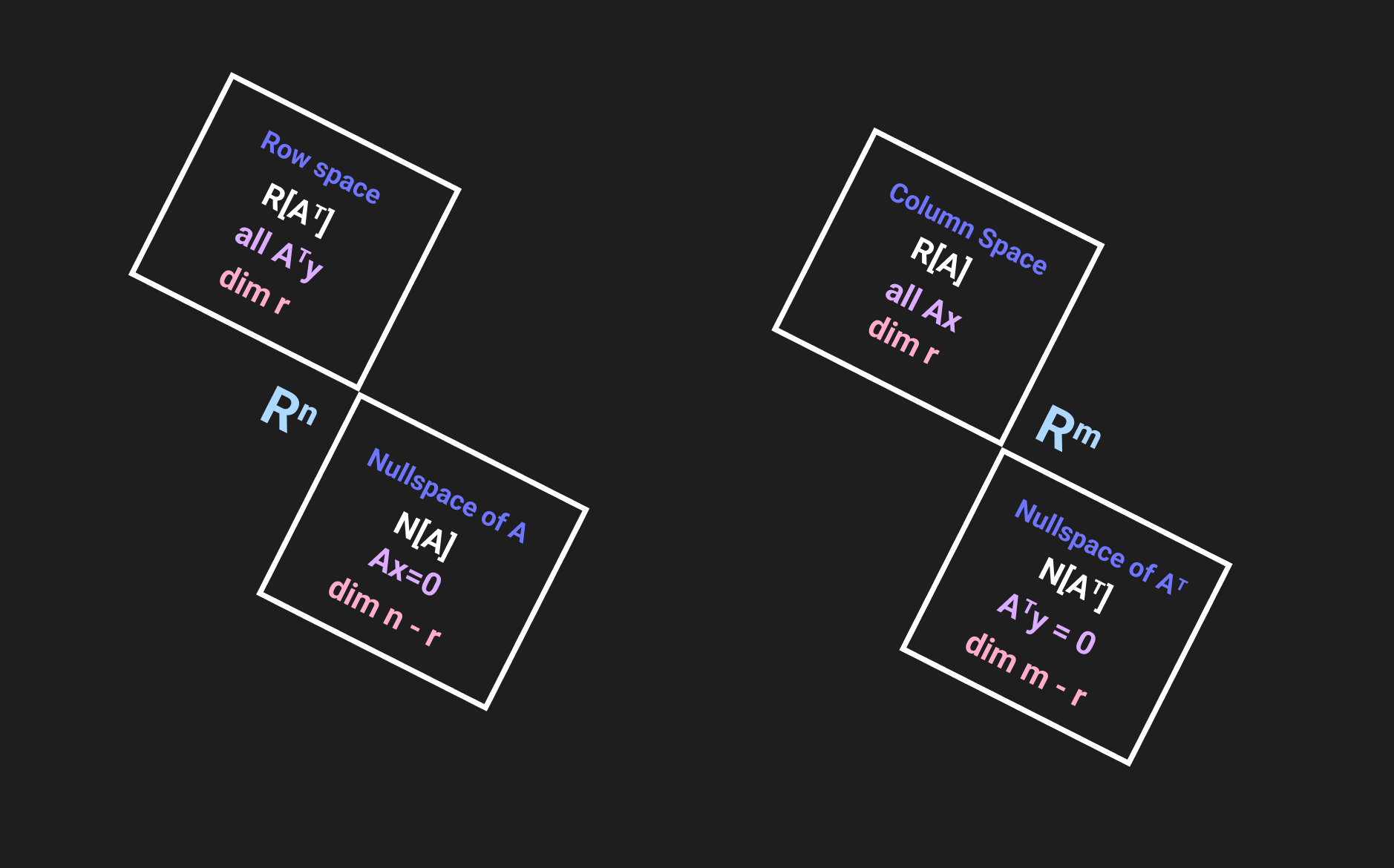
Exercises

Let \(A = LU\) be the LU decomposition of \(A\). Determine whether the statement is True or False.

• \(N(A^T) = N(U^T)\)

• \(R(A^T) = R(U^T)\)

Solution

• False

• True

Let \(A\) be a \(m \times n\) matrix and let \(\{ \boldsymbol{u}_1,\boldsymbol{u}_2 \} \subset \mathbb{R}^n\) be a basis of the nullspace \(N(A)\). Determine \(\dim(R(A^T))\) and \(\dim(N(A^T))\).

Solution

\(\dim(R(A^T)) = n-2\) and \(\dim(N(A^T)) = m-n+2\).

Let \(A\) be a \(4 \times 4\) matrix such that

\[\begin{split} A = LU = \left[ \begin{array}{rrrrrr} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 2 & 1 & 1 \end{array} \right] \left[ \begin{array}{rrrrrr} 1 & -1 & 2 & -1 \\ 0 & 1 & -3 & 4 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right] \end{split}\]

Find a basis of \(N(A^T)\) and find a basis of \(R(A^T)\).

Solution

\[\begin{split} N(A^T) = \mathrm{span} \left\{ \left[ \begin{array}{r} 1 \\ -1 \\ -1 \\ 1 \end{array} \right] \right\} \hspace{10mm} R(A^T) = \mathrm{span} \left\{ \left[ \begin{array}{r} 1 \\ -1 \\ 2 \\ -1 \end{array} \right] , \left[ \begin{array}{r} 0 \\ 1 \\ -3 \\ 4 \end{array} \right] , \left[ \begin{array}{r} 0 \\ 0 \\ 0 \\ 1 \end{array} \right] \right\} \end{split}\]

Let \(A\) be a matrix such that its LU decomposition is of the form

\[\begin{split} A = LU = \begin{bmatrix} 1 & 0 & 0 \\ * & 1 & 0 \\ * & * & 1 \end{bmatrix} \begin{bmatrix} * & * & * & * \\ 0 & * & * & * \\ 0 & 0 & 0 & * \end{bmatrix} \end{split}\]

where \(*\) denotes a nonzero number. Determine the dimension of \(R(A^T)\) and the dimension of \(N(A^T)\).

Solution

\(\dim(R(A^T)) = 3\) and \(\dim(N(A^T)) = 0\)