Error Analysis

The condition number of a nonsingular matrix \(A\) is \(\mathrm{cond}(A) = \| A \| \| A^{-1} \|\). Given a linear system \(A \boldsymbol{x} = \boldsymbol{b}\), the condition number of \(A\) quantifies how sensitive the solution \(\boldsymbol{x}\) is relative to changes in \(\boldsymbol{b}\).

Vector Norms

The Euclidean norm of a vector \(\boldsymbol{x} \in \mathbb{R}^n\) is

\[ \| \boldsymbol{x} \| = \sqrt{ | x_1|^2 + \cdots + | x_n |^2 } = \sqrt{ \sum_{k=1}^n | x_k |^2 } \]

The Euclidean norm assigns a magnitude (or length) to a vector but it turns out that there are many different ways to define the “magnitude” of a vector!

A norm on \(\mathbb{R}^n\) is a function \(\| \cdot \|\) such that:

1. \(\| \boldsymbol{x} \| \geq 0\) for all \(\boldsymbol{x} \in \mathbb{R}^n\)

2. \(\| \boldsymbol{x} \| = 0\) if and only if \(\boldsymbol{x} = \boldsymbol{0}\)

3. \(\| c \boldsymbol{x} \| = |c| \| \boldsymbol{x} \|\) for any \(c \in \mathbb{R}\) and \(\boldsymbol{x} \in \mathbb{R}^n\)

4. \(\| \boldsymbol{x} + \boldsymbol{y} \| \leq \| \boldsymbol{x} \| + \| \boldsymbol{y} \|\) for all \(\boldsymbol{x} , \boldsymbol{y} \in \mathbb{R}^n\)

Condition 4 is called the triangle inequality. See Wikipedia:Norm.

Let \(1 \leq p < \infty\). The \(p\)-norm of a vector \(\boldsymbol{x} \in \mathbb{R}^n\) is given by

\[ \| \boldsymbol{x} \|_p = \left( \sum_{k=1}^n | x_k |^p \right)^{1/p} \]

In particular, the 1-norm is given by

\[ \| \boldsymbol{x} \|_1 = | x_1 | + \cdots + | x_n | \]

and the 2-norm is the familiar Euclidean norm

\[ \| \boldsymbol{x} \|_2 = \sqrt{ | x_1|^2 + \cdots + | x_n |^2 } \]

The \(\infty\)-norm of a vector \(\boldsymbol{x} \in \mathbb{R}^n\) is given by

\[ \| \boldsymbol{x} \|_{\infty} = \max \{ | x_1| , \dots , | x_n | \} \]

The unit sphere in \(\mathbb{R}^n\) relative to a norm \(\| \cdot \|\) is the set of unit vectors

\[ B = \{ \boldsymbol{x} \in \mathbb{R}^n : \| \boldsymbol{x} \| = 1 \} \]

Compare the unit balls in \(\mathbb{R}^2\) for the 1-norm, 2-norm and \(\infty\)-norm:

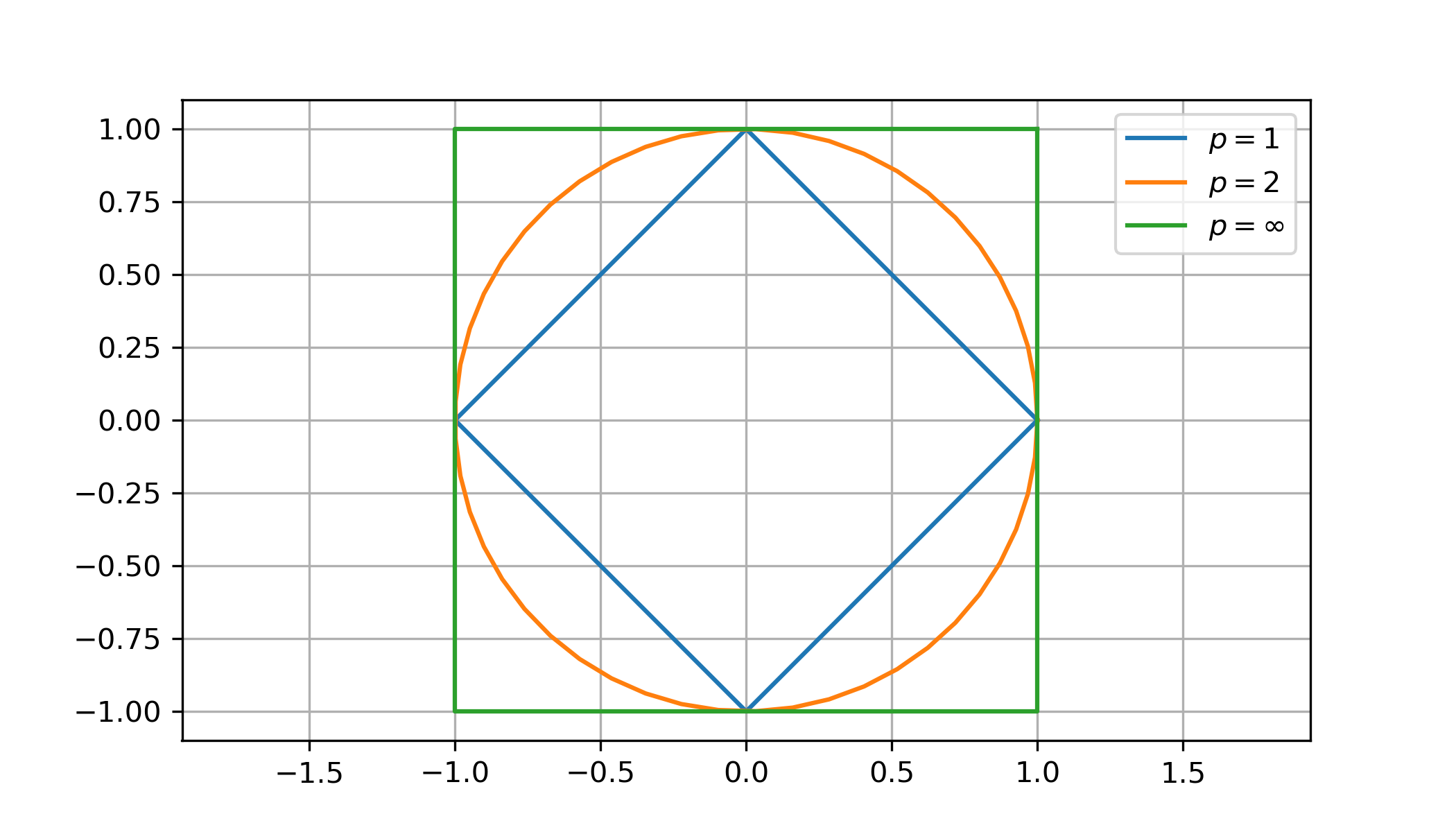
The most commonly used vector norm is the 2-norm. If we use the notation \(\| \boldsymbol{x} \|\) then we assume it is the 2-norm unless explicitly stately otherwise.

Matrix Norms

A matrix norm is a function on matrices that satisfies the properties:

1. \(\| A \| > 0\) for all \(A \not= 0\)

2. \(\| A \| = 0\) if and only \(A = 0\)

3. \(\| c A \| = |c| \| A \|\) for any \(c \in \mathbb{R}\)

4. \(\| A + B \| \leq \| A \| + \| B \|\)

5. \(\| A B \| \leq \| A \| \| B \|\)

See Wikipedia: Matrix norm.

The Frobenius norm of a matrix \(A\) is given by

\[ \| A \|_F = \sqrt{ \sum_{i=1}^{m} \sum_{j=1}^{n} |a_{i,j}|^2 } \]

where \(a_{i,j}\) are the entries of \(A\)

\[\begin{split} A = \begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{bmatrix} \end{split}\]

The operator norm of a matrix \(A\) is given by

\[ \| A \| = \max_{\boldsymbol{x} \not= \boldsymbol{0} } \frac{ \| A \boldsymbol{x} \| }{ \| \boldsymbol{x} \|} \]

where \(\| \cdot \|\) is the 2-norm.

The operator norm satisies the property \(\| A \boldsymbol{x} \| \leq \| A \| \| \boldsymbol{x} \|\) for all \(\boldsymbol{x} \in \mathbb{R}^n\).

An operator norm is a matrix norm.

The operator norm and the previous result gives us most of the matrix norms used in practice.

Let \(A\) be a nonsingular matrix. Then

\[ \| A \| = \max_{ \| \boldsymbol{x} \| = 1 } \| A \boldsymbol{x} \| \hspace{10mm} \text{and} \hspace{10mm} \| A^{-1} \| = \frac{1}{ \displaystyle \min_{ \| \boldsymbol{x} \| = 1 } \| A \boldsymbol{x} \|} \]

In other words, \(\| A \|\) is the maximum stretch of a unit vector by the linear transformation \(A\), and \(\| A^{-1} \|\) is the reciprocal of the minimum stretch of a unit vector by the linear transformation \(A\).

Proof

Note that \(\| A \boldsymbol{x} \| / \| \boldsymbol{x} \|= \| A ( \boldsymbol{x} / \| \boldsymbol{x} \| ) \|\) therefore

\[ \| A \| = \max_{ \| \boldsymbol{x} \| = 1 } \| A \boldsymbol{x} \| \]

Similarly, we can rearrange the definition of \(\| A^{-1} \|\) to find:

\[\begin{split} \begin{align*} \| A^{-1} \| &= \max_{ \boldsymbol{x} \not= 0} \frac{\| A^{-1} \boldsymbol{x} \|}{\| \boldsymbol{x} \|} \\ &= \max_{ \boldsymbol{x} \not= 0} \frac{\| A^{-1} A \boldsymbol{x} \|}{\| A \boldsymbol{x} \|} \\ &= \max_{ \boldsymbol{x} \not= 0} \frac{\| \boldsymbol{x} \|}{\| A \boldsymbol{x} \|} \\ &= \max_{ \| \boldsymbol{x} \| = 1} \frac{1}{\| A \boldsymbol{x} \|} \\ &= \frac{1}{\displaystyle \min_{ \| \boldsymbol{x} \| = 1} \| A \boldsymbol{x} \|} \end{align*} \end{split}\]

Let \(D\) be a diagonal matrix and let \(\boldsymbol{d}\) be the vector of diagonal entries of \(D\):

\[\begin{split} D = \begin{bmatrix} d_1 & & & \\ & d_2 & & \\ & & \ddots & \\ & & & d_n \end{bmatrix} \hspace{10mm} \boldsymbol{d} = \begin{bmatrix} d_1 \\ d_2 \\ \vdots \\ d_n \end{bmatrix} \end{split}\]

Then \(\| D \| = \| \boldsymbol{d} \|_{\infty} = \max \{ |d_1| , \dots, |d_n| \}\), and \(\| D \|_F = \| \boldsymbol{d} \|_2\).

Proof

Compute

\[\begin{split} \begin{align*} \| D \| &= \max_{\| \boldsymbol{x} \| = 1} \| D \boldsymbol{x} \| \\ &= \max_{\| \boldsymbol{x} \| = 1} \sqrt{d_1^2 x_1^2 + \cdots + d_n^2 x_n^2} \\ &\leq \max_{\| \boldsymbol{x} \| = 1} \left( \max_i \{ | d_i | \} \right) \sqrt{ x_1^2 + \cdots + x_n^2} \\ &= \max_i \{ | d_i | \} \end{align*} \end{split}\]

The equality \(\| D \|_F = \| \boldsymbol{d} \|_2\) is clear.

How do we compute the matrix norm \(\| A \|\) for a general matrix? This is a nontrivial problem and we will see later how to use the singular values of \(A\) to determine the matrix norm.

Condition Number

The condition number of a nonsingular square matrix \(A\) is

\[ \mathrm{cond}(A) = \| A \| \| A^{-1} \| \]

By convention, we define \(\mathrm{cond}(A) = \infty\) if \(\det(A) = 0\).

If \(A\) is nonsingular, we have

\[ \mathrm{cond}(A) = \| A \| \| A^{-1} \| = \frac{\text{maximum stretch of a unit vector}}{\text{minimum stretch of a unit vector}} \]

The image below shows the unit circle and its image under the linear transformation defined by a \(2 \times 2\) matrix \(A\). Determine \(\| A \|\), \(\| A^{-1} \|\) and \(\mathrm{cond}(A)\).

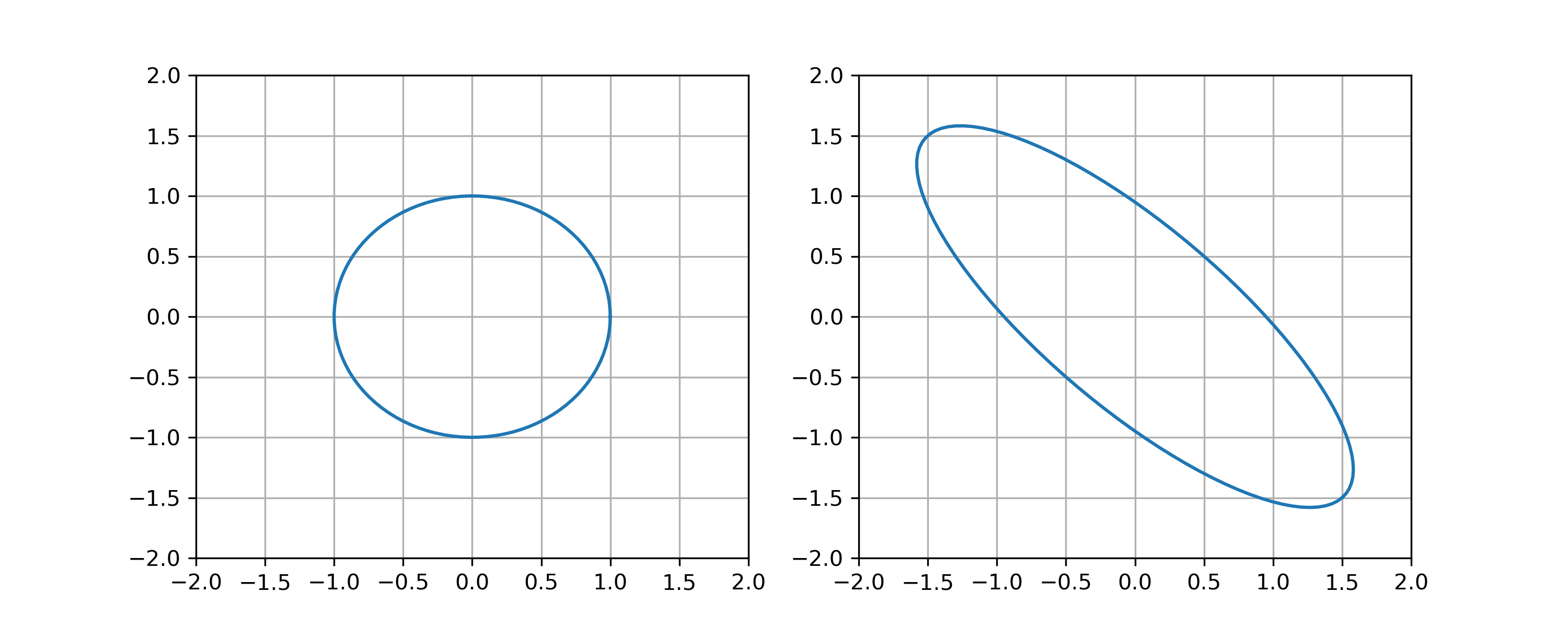
Observe the maximum stretch of a unit vector is \(\| A \| = 3 / \sqrt{2}\), the minimum stretch is \(1/\sqrt{2}\) therefore \(\| A^{-1} \| = \sqrt{2}\) and the condition number is \(\mathrm{cond}(A) = 3\).

Relative Errors

Let \(A\) be a nonsingular matrix and consider the linear system \(A \boldsymbol{x} = \boldsymbol{b}\). If a small change \(\Delta \boldsymbol{b}\) corresponds to a change \(\Delta \boldsymbol{x}\) in the sense that \(A(\boldsymbol{x} + \Delta \boldsymbol{x}) = \boldsymbol{b} + \Delta \boldsymbol{b}\), then

\[ \frac{\| \Delta \boldsymbol{x} \|}{\| \boldsymbol{x} \|} \leq \mathrm{cond}(A) \frac{\| \Delta \boldsymbol{b} \|}{\| \boldsymbol{b} \|} \]

Proof

Since \(A \boldsymbol{x} = \boldsymbol{b}\), we have \(\Delta x = A^{-1} \Delta \boldsymbol{b}\). Computing norms we find

\[\begin{split} \begin{align*} \| \boldsymbol{b} \| &= \| A \boldsymbol{x} \| \\ & \\ \| \Delta \boldsymbol{x} \| \| \boldsymbol{b} \| &= \| A^{-1} \Delta \boldsymbol{b} \| \| A \boldsymbol{x} \| \\ & \\ \| \Delta \boldsymbol{x} \| \| \boldsymbol{b} \| &\leq \| A^{-1} \| \| \Delta\boldsymbol{b} \| \| A \| \| \boldsymbol{x} \| \\ & \\ \frac{\| \Delta \boldsymbol{x} \|}{ \| \boldsymbol{x} \|} &\leq \| A \| \| A^{-1} \| \frac{\| \Delta \boldsymbol{b} \|}{\| \boldsymbol{b} \|} \end{align*} \end{split}\]

Given a vector \(\boldsymbol{b}\) and small change \(\Delta \boldsymbol{b}\), the relative change (or relative error) is

\[ \frac{\| \Delta \boldsymbol{b} \|}{\| \boldsymbol{b} \|} \]

The error bound

\[ \frac{\| \Delta \boldsymbol{x} \|}{\| \boldsymbol{x} \|} \leq \mathrm{cond}(A) \frac{\| \Delta \boldsymbol{b} \|}{\| \boldsymbol{b} \|} \]

implies that if \(A\) has a large condition number then small changes in \(\boldsymbol{b}\) may result in very large changes in the solution \(\boldsymbol{x}\). In other words, the solution \(\boldsymbol{x}\) is sensitive to errors in \(\Delta \boldsymbol{b}\).

Exercises

Show that the 1-norm satisfies the properties of a norm.

Solution

We need to show that the 1-norm satisfies all four properties of a vector norm:

1. \(||x||_1 = |x_1| + |x_2| + ... + |x_n| \geq 0\) for any \(x \in \mathbb{R}^n\)

2. \(||x||_1 = |x_1| + |x_2| + ... + |x_n| = 0 \iff |x_1| = |x_2| = ... = |x_n| = 0 \)

3. \(||cx||_1 = |cx_1| + |cx_2| + |cx_3| + ... + |cx_n| = |c|(|x_1| + |x_2| + ... + |x_n|) = |c|||x||_1\) for any \(c \in \mathbb{R}\)

4. \(||x + y||_1 = |x_1 + y_1| + |x_2 + y_2| + ... + |x_n + y_n| \leq |x_1| + |y_1| + |x_2| + |y_2| + ... + |x_n| + |y_n| = ||x||_1 + ||y||_1\) for any \(x, y \in \mathbb{R}^n\)

Show that the \(\infty\)-norm satisfies the properties of a norm.

Solution

We need to show that the \(\infty\)-norm satisfies all four properties of a vector norm:

1. \(||x||_{\infty} = \max\{|x_1|, |x_2|, ..., |x_n|\} \geq 0\) for any \(x \in \mathbb{R}^n\)

2. \(||x||_{\infty} = \max\{|x_1|, |x_2|, ..., |x_n|\} = 0 \iff |x_1| = |x_2| = ... = |x_n| = 0 \)

3. \(||cx||_{\infty} = \max\{|cx_1|, |cx_2|, ..., |cx_n|\} = |c|\max\{|x_1|, |x_2|, ..., |x_n|\} = |c|||x||_{\infty}\) for any \(c \in \mathbb{R}\)

4. \(||x + y||_{\infty} = \max\{|x_1 + y_1|, |x_2 + y_2|, ..., |x_n + y_n|\} \leq \max\{|x_1| + |y_1|, |x_2| + |y_2|, ..., |x_n| + |y_n|\} = ||x||_{\infty} + ||y||_{\infty}\) for any \(x, y \in \mathbb{R}^n\)

Is the function \(\| \boldsymbol{x} \| = x_1 + \cdots + x_n\) a vector norm? Explain.

Solution

It is not. We can show that it violates the 2nd condition of a norm.

Choose the vector \(x = (1,-1,0,\cdots,0)\), we have the “norm”:

\[||x|| = 1 + (-1) + 0 + \cdots + 0 = 0\]

The function

\[ \| \boldsymbol{x} \|_p = \left( \sum_{k=1}^n | x_k |^p \right)^{1/p} \]

does not satisfy the triangle inequality if \(0 < p < 1\). Prove this for \(n=2\) and \(p=0.5\). In other words, find vectors \(\boldsymbol{x},\boldsymbol{y} \in \mathbb{R}^2\) such that

\[ \| \boldsymbol{x} + \boldsymbol{y} \|_{0.5} > \| \boldsymbol{x} \|_{0.5} + \| \boldsymbol{y} \|_{0.5} \]

Is it true that \(\| \boldsymbol{x} \|_1 \leq \| \boldsymbol{x} \|_2 \leq \| \boldsymbol{x} \|_{\infty}\) for all \(\boldsymbol{x} \in \mathbb{R}^n\)? Explain.

Solution

This is not true. The correct inequalities are:

\[ \| \boldsymbol{x} \|_{\infty} \leq \| \boldsymbol{x} \|_2 \leq \| \boldsymbol{x} \|_1 \]

Proof: \( \| \boldsymbol{x} \|_{\infty} = \max \{ |x_1|, |x_2|, ..., |x_n| \} \leq \sqrt{x_1^2 + x_2^2 + ... + x_n^2} = \| \boldsymbol{x} \|_2 \) by the Cauchy-Schwarz inequality.

Additionally, \( \| \boldsymbol{x} \|_2 = \sqrt{x_1^2 + x_2^2 + ... + x_n^2} \leq |x_1| + |x_2| + ... + |x_n| = \| \boldsymbol{x} \|_1 \) by the triangle inequality.

Therefore, \(\| \boldsymbol{x} \|_{\infty} \leq \| \boldsymbol{x} \|_2 \leq \| \boldsymbol{x} \|_1\).

Determine whether the statement is True or False: If \(\| A \| = 1\) then \(A = I\).

Solution

This is false, but the converse is true.

We can give a counterexample with the following diagonal matrix with the max diagonal entry of 1:

\(A = \begin{pmatrix} 0.5 & 0 \\ 0 & 1 \end{pmatrix} \Longrightarrow ||A|| = 1\) but \(A \neq I_2\)

We can come up with similar diagonal matrices for the \(n \times n\) case.

Suppose \(A\) is a 2 by 2 matrix such that the image of the unit circle under the linear transformation \(A\) is:

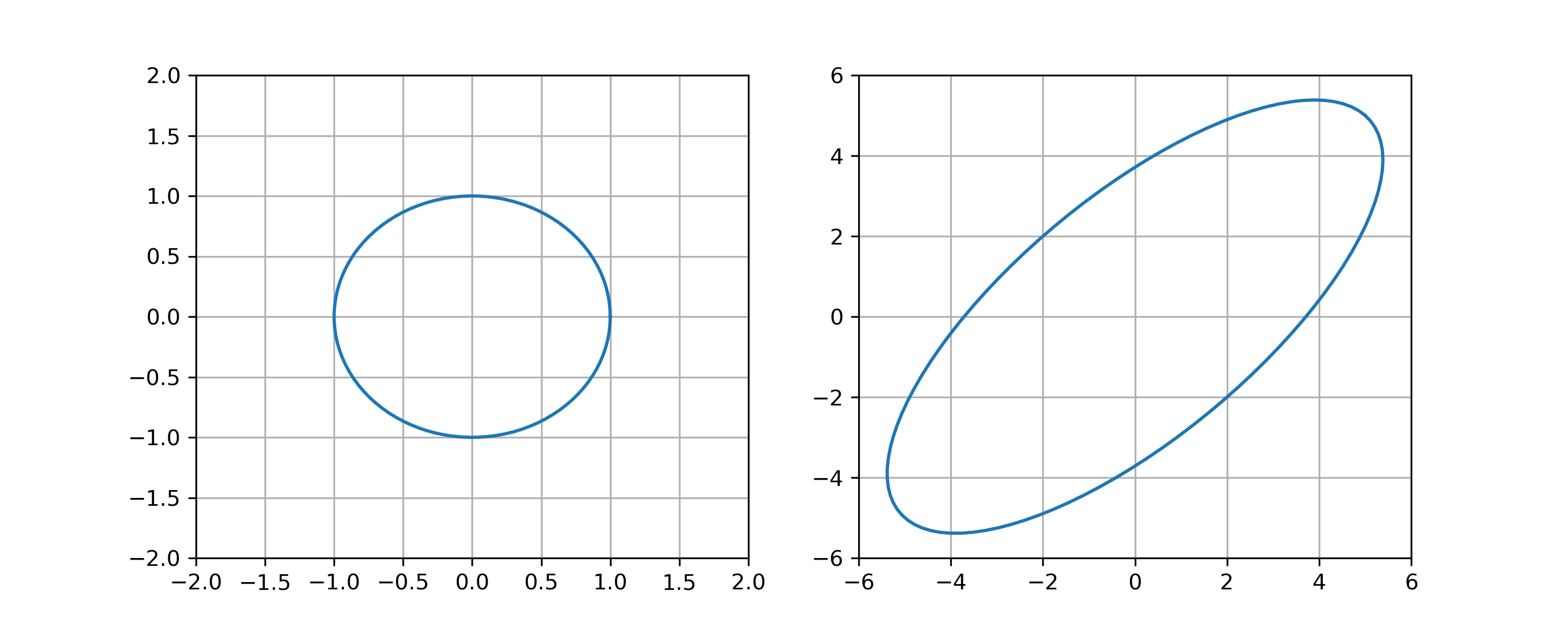
Determine \(\mathrm{cond}(A)\) with respect to the 1, 2, and \(\infty\) norm.

Solution

We begin by computing the operator norm with respect to the 2 -norm. From the definition of the operator norm we have

\[ \|A\|=\max _{\|x\|_{2}=1}\|A x\|_{2} \]

Since the values in the left plot are exactly those on the unit sphere we must only identify the vector \(A x\) that has been stretched the most i.e. \(A x=(5,5)\) Thus

\[ \|A\|_{2}=5 \sqrt{2} \]

Similarly for \(\left\|A^{-1}\right\|\) the vector least stretched is \(A x=(-2,2)\) thus

\[ \left\|A^{-1}\right\|_{2}=\frac{1}{2 \sqrt{2}} \]

So that we find that

\[ \operatorname{cond}(A)_2=\frac{5}{2} \]

For the 1 and \(\infty\) norm, we realize that the vectors \(v_{1}=\frac{1}{\sqrt{2}}(1,1)\) and \(v_{2}=\frac{1}{\sqrt{2}}(-1,1)\) are eigenvectors i.e.

\[ A v_{1}=(5,5)=5 \sqrt{2} \frac{1}{\sqrt{2}}(1,1), \quad A v_{2}=(-2,2)=2 \sqrt{2} \frac{1}{\sqrt{2}}(-1,1) \]

Thus we have the diagonalization:

\[\begin{split} A = PD P^{-1} = \begin{pmatrix}5 & 2 \\5 & -2 \end{pmatrix}\begin{pmatrix}5\sqrt{2} & 0 \\0 & 2\sqrt{2} \end{pmatrix}\begin{pmatrix}\frac{1}{10} & \frac{1}{10} \\\frac{1}{4} & -\frac{1}{4} \end{pmatrix} = \frac{1}{\sqrt{2}}\begin{pmatrix}7 & 3 \\ 3 & 7 \end{pmatrix} \end{split}\]

and the inverse

\[\begin{split} A^{-1} = \frac{1}{20\sqrt{2}}\begin{pmatrix}7 & -3 \\ -3 & 7 \end{pmatrix} \end{split}\]

Then, we compute the condition number:

\[ \operatorname{cond}(A)_1 = \operatorname{cond}(A)_{\infty} = \|A\|_{\infty} \|A^{-1}\|_{\infty} = \left(\frac{10}{\sqrt{2}} \right)\left(\frac{10}{20\sqrt{2}} \right) = \frac{5}{2} \]